The given information is:
The starting population of bacteria is 390.
The population quadruples every 20 minutes.
To find the equation of the population in terms of minutes, we can apply the following formula:
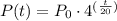
Where P0 is the starting population, the number 4 is because the population quadruples every 20 minutes (the 20 in the power is given by this), it is equal to 4 times the initial number, and t is the time in minutes.
If we replace the known values, we obtain:
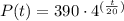
To find the population after 1 hour, we need to convert 1 hour to minutes, and it is equal to 60 minutes, then we need to replace t=60 in the formula and solve:

Thus, after 1 hour there are 24960 bacterias.