Since the runner completes 1 lap in 314 seconds, and its velocity is 3.1m/s, then the total distance covered in 1 lap is:
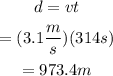
That distance corresponds to the perimeter of the circumference. The perimeter of a circumference with radius r is 2πr. Then:
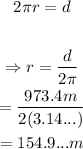
The centripetal acceleration of an object in a circular trajectory with radius r and speed v is:
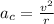
Replace v=3.1m/s and r=154.9m to find the centripetal acceleration:
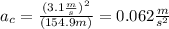
Therefore, the radius of the track is approximately 155m and the centripetal acceleration of the runner is approximately 0.062 m/s^2.