SOLUTION
Given the question, the following are the solution steps to answer the question.
STEP 1: Write the formula for the area of the triangle
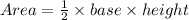
STEP 2: Represent the statements to get an equation

STEP 3: Substitute into the formula in step 1
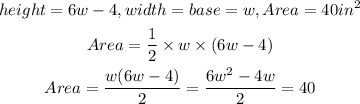
STEP 4: Cross multiply

STEP 5: Find the values of w
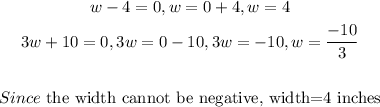
STEP 6: Find the height
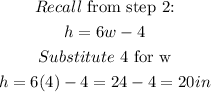
Hence,
width = 4 inches
height = 20 inches