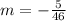Answer:
The slope m of the line that passes through the two given points is;
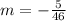
Step-by-step explanation:
We want to calculate the slope of the line that passes through the given point;
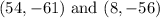
Recall that the slope formula can be written as;

substituting the given points;
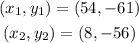
We have;

Therefore, the slope m of the line that passes through the two given points is;