Question

. In a 30°-60-90° triangle, the hypotenuse is 7 yards long.Find the exact lengths of the legs?

Answer 1

The lengths of the legs of the triangle are 6.06 yards and 3.6 yards.

Step-by-step explanation

First, let us make a sketch of the problem:

To find the length of the legs, we have to apply trigonometric ratios SOHCAHTOA.

We have that:

`\sin (60)=\frac{\text{opposite}}{\text{hypotenuse}}`

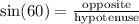
From the diagram:

`\begin{gathered} \sin (60)=(x)/(7) \\ \Rightarrow x=7\cdot\sin (60) \\ x\approx6.06\text{ yds} \end{gathered}`

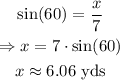
We also have that:

`\sin (30)=\frac{\text{opposite}}{\text{hypotenuse}}`

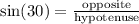
From the diagram:

`\begin{gathered} \sin (30)=(y)/(7) \\ \Rightarrow y=7\cdot\sin (30) \\ y=3.5\text{ yds} \end{gathered}`

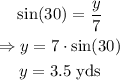
The lengths of the legs of the triangle are 6.06 yards and 3.5 yards.