Question

How much should be invested now at an interest rate of 7% per year, compounded continuously, to have 2000 dollars in three years? Do not round intermediate computations, and round your answer to the nearest cent

Answer 1

The amount that should be invested is $1621.16

Step-by-step explanation:

The formula for continuous compound interest is:

`A=Pe^(rt)`

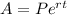
Where:

A is the amount of money after t years

P is the invested amount (what we want to find, in this case)

r is the rate of compounding in decimal

t i the amount of time compounding, in years

Then, in this case:

A = $2000

r = 0.07 (to convert percentage to decimal, we divide by 100: 7% / 100 = 0.07)

t = 3 years

Then:

`2000=Pe^(0.07\cdot3)`
`2000=Pe^(0.21)`

`P=(2000)/(e^(0.21))\approx1621.16849`

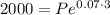
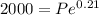
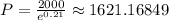
To the nearest cent, P = $1621.16