If we have 2 endpoints (x1, y1) and (x2, y2), the coordinates of the midpoint will be:
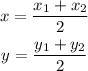
Now, we know the coordinates of one endpoint (x1, y1) equal to (-8, -1) and the midpoint (x, y) equal to (0,3), so we can replace those values and solve for x2 and y2.
Then, for the x-coordinate, we get:
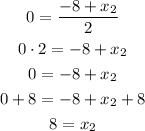
At the same way, for the y-coordinate, we get:
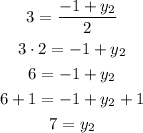
Therefore, the coordinates of the other endpoint are (8, 7)
Answer: (8, 7)