Question

LanaCharles almn on the coordinate plane what is the perimeter of a ALMN round to the nearest unit

Answer 1

The Solution:

Given the graph below:

We are required to find the perimeter of the triangle LMN rounded to the nearest unit.

Step 1:

Find the distance LM, where L(-3,2) and M(3,5)

By the formula for distance between two points, we have

`LM=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Where,

`\begin{gathered} x_1=-3 \\ y_1=2 \\ x_2=3 \\ y_2=5 \end{gathered}`

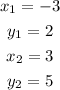
Substituting, we get

`LM=\sqrt[]{(3--3)^2+(5-2)^2}=\text{ }\sqrt[]{6^2+7^2}=\text{ }\sqrt[]{85}=9.2195`

Step 2:

Find the distance LN:

`LN=12`

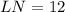
Step 3:

Find the distance MN, where M(3,5) and N(9,2)

`MN=\sqrt[]{(9-3)^2+(2-5)^2}=\text{ }\sqrt[]{6^2+(-3)^2}=\text{ }\sqrt[]{45}=6.7082`

Step 4:

The perimeter is:

`\text{ Perimeter=LM+MN+LN=9.2195+6.7082+12=27.9277}\approx28\text{ units}`

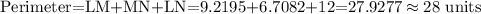
Therefore, the correct answer is 28 units.