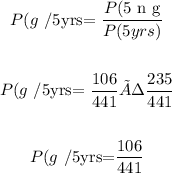Question

Out of 441 applicants for a job 235 have over five years of experience and 106 have over five years of experience and have a graduate degreeWhat is the probability that a randomly chosen applicant has a graduate degree given that they have a five years of experience enter a fraction or round your answer to four decimal places if necessary

Answer 1

Answer:

Probability that a randomly chosen applicant has a graduate degree given that they have a five years of experience = 106/441

Step-by-step explanation:

Total number of applicants, n(Total) = 441

Number of candidates that have over five years of experience, n(5 yrs) = 235

Probability that a randomly chosen applicant has over 5 years experience

`\begin{gathered} P(5yrs)=(n(5yrs))/(n(Total)) \\ \\ P(5yrs)=(235)/(441) \end{gathered}`

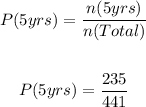
Number of applicants that have over five years of experience and have a graduate degree, n(5 n g) = 106

Probability that a randomly selected applicant has over five years of experience and have a graduate degree

`\begin{gathered} P(5\text{ n g\rparen = }\frac{n(5\text{ n g\rparen}}{n(Total)} \\ \\ P(5\text{ n g\rparen = }(106)/(441) \end{gathered}`

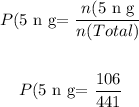
Probability that a randomly chosen applicant has a graduate degree given that they have a five years of experience

`\begin{gathered} P(g\text{ /5yrs\rparen = }\frac{P(5\text{ n g\rparen}}{P(5yrs)} \\ \\ P(g\text{ /5yrs\rparen = }(106)/(441)÷(235)/(441) \\ \\ P(g\text{ /5yrs\rparen=}(106)/(441) \end{gathered}`