Question

A motorboat takes 3 hours to travel 108 miles going upstream. The return trip takes 2 hours going downstream. What is the rate in still water and what is the rate of the current?Rate of the boat in still water: mi/hRate of the current: mi/hmi/h= miles per hour

Answer 1

Given:

It takes the boat 3 hours to travel 108 miles going upstream

Return trip = 2hours going downstream

Distance, d = 108 miles

Time going upstream = 3 hours

Time going downstream = 2 hours

Let's find the rate in still water and the current rate.

Let s represent the still rate

Let c represent the current rate.

Apply the distance formula:

Distance = Rate x Time

We have the set of equations:

(s - c) x 3 = 108.................................Equation 1

(s + c) x 2 = 108.................................Equation 2

Apply distributive property:

3s - 3c = 108

2s + 2c = 108

Let's solve both equations simultaneously using substitution method.

Rewrite the first equation for s:

3s - 3c = 108

Add 3c to both sides:

3s - 3c + 3c = 108 + 3c

3s = 108 + 3c

Divide all terms by 3:

`\begin{gathered} (3s)/(3)=(108)/(3)+(3c)/(3) \\ \\ s=36+c \end{gathered}`

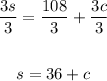
Substitute s for (36 + c) in equation 2:

2s + 2c = 108

2(36 + c) + 2c = 108

72 + 2c + 2c = 108

72 + 4c = 108

Subtract 72 from both sides:

72 - 72 + 4c = 108 - 72

4c = 36

Divide both sides by 4:

`\begin{gathered} (4c)/(4)=(36)/(4) \\ \\ c=9 \end{gathered}`

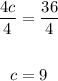
Substitute c for 9 in either of thee equation.

Take the first equation:

3s - 3c = 108

3s - 3(9) = 108

3s - 27 = 108

Add 27 to both sides:

3s - 27 + 27 = 108 + 27

3s = 135

Divide both sides by 3:

`\begin{gathered} (3s)/(3)=(135)/(3) \\ \\ s=45 \end{gathered}`

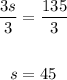
Thus, we have the solutions:

c = 9

s = 45

The rate of boat in still water is 45 miles per hour

The rate of the current is 9 miles per hour

Therefore, we have:

Rate of boat in still water: 45 mi/h

Rate of current: 9 mi/h

Take the firs

ANSWER:

Rate of boat in still water: 45 mi/h

Rae of the current: 9 mi/h