occur
the answer is 12/13 or 0.932
Step-by-step explanation
when you have an event A, the complement of A, denoted by.
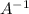
consists of all the outcomes in wich the event A does NOT ocurr
it is given by:
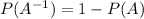
Step 1
find the probability of event A :(P(A)
The probability of an event is the number of favorable outcomes divided by the total number of outcomes possible
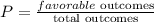
so
let
favorable outcome = 4 (there are four 7 in the deck)
total outcomes=52
hence,replacing
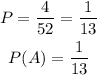
Step 2
now, to find the probability that the event does NOT ocurrs ( not drawing a 7)
let's apply the formula
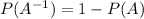
replace
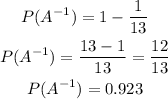
therefore, the answer is 12/13 or 0.932
I hope this helps you