Question

I haven’t came across one of these questions so not sure how to solve

Answer 1

m∠F = 140º

1) Since that trapezoid is a quadrilateral, then we can affirm that the Sum of their interior angles is:

`\begin{gathered} S_i=180(n-2) \\ S_i=180(4-2) \\ S_i=180(2) \\ S_i=360 \end{gathered}`

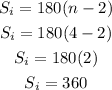
Note that "n" refers to the number of sides:

Notice also that angle H is a right angle since this is not an Isosceles Trapezoid

So we can write out the following

9x +14x +4x + 90 = 360º

27x = 360 -90

27x = 270

x =10

Alternatively, angles between parallel lines are supplementary

2) To find out the measure of angle ∠F We'll need to plug x=10 into that expression:

m∠F = 14x

m∠F = 140º