To solve the system of equations
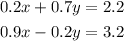
we need to make the coefficients of one of the variables opposite, that is, they need to have the same value with different sign; let's do this with the y variable, so let's multiply the second equation by 0.7 and the first equation by 0.2; then we have:
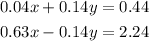
Now we add the equations and solve the resulting equation for x:
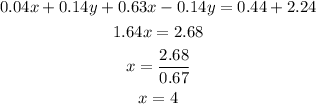
Now that we have the value of x we plug it in one of the original equations and solve for y:
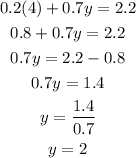
Therefore, the solution of the system of equation is (4,2)