Question

It took 89.5 degrees to stop the wheel from 47.8 rpm. What is the angular acceleration?

Answer 1

Given:

The angular displacement, θ=89.5°

Initial angular velocity, ω₀=47.8 rpm

Final angular velocity, ω=0 rad/s

To find:

The angular acceleration of the wheel.

Step-by-step explanation:

The angular velocity can be converted to rad/s as,

`\begin{gathered} \omega_0=(47.8*2\pi)/(60) \\ =5\text{ rad/s} \end{gathered}`

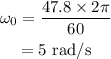
The angle is converted into the radians as,

`\begin{gathered} \theta=(89.5*\pi)/(180) \\ =1.56\text{ rad} \end{gathered}`

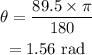
From the equation of motion,

`\omega^2-\omega^2=2\alpha\theta`

Where α is the angular acceleration of the wheel.

On substituting the known values,

`\begin{gathered} 0^2-5^2=2*\alpha*1.56 \\ \implies\alpha=(-5^2)/(2*1.56) \\ =-8.01\text{ rad/s}^2 \end{gathered}`

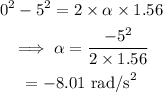
Final answer:

Thus the angular acceleration of the wheel is -8.01 rad/s²