Question

How many ways can Rudy choose 4 pizza toppings from a menu of 16 toppings if each can only be chosen once

Answer 1

1820 different ways

Explanation:

We can use here combination rule for selection:

`_nC_r=(n!)/(r!(n-r)!)`

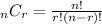
In this case n is equal to 16 and r is equal to 4, therefore, replacing and calculating the number in different ways, there:

`\begin{gathered} _(16)C_4=(16!)/(4!(16-4)!)=(16!)/(4!\cdot12!) \\ \\ _(16)C_4=1820 \end{gathered}`

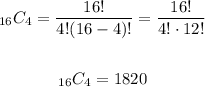
So in total there are 1820 different ways Rudy can choose 4 pizza toppings.