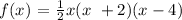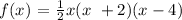
Step-by-step explanation:
To detrmine the formula of the polynomial, we check for the roots on the graph:
when y = 0, x = -2
when y = 0, x = 4
We have two roots.
x = -2
x + 2 = 0
x = 4
x - 4 = 0
3rd factor is x = 0
Hence, we have two factors: x(x + 2) and (x - 4)
The polynomial function using the factors:

Next, we find the value of a:
To get a , we pick a point on the graph. let the point be (0, -4)
substitute the point in the function above:
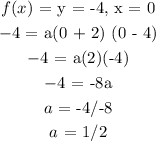
The formula of the polynomial becomes: