Question

Identify the side lengths that form a right triangle.a. 12, 13, 16b. 15, 20, 21c. 9, 40, 42d. 10, 24, 26Identify the side lengths that form a right triangle.a. 3, 4, 8b. 30, 40, 45c. 5, 12, 13d. 6, 12, 133. do the side lengths of 8, 10, and 13 form a right triangle? 4. Determine if ▼ABC is a right triangle if AB=36, AC=48 and BC=60

Answer 1

d. 10, 24, 26

Step-by-step explanation:

To identify the side lengths that form a right triangle, we check if it satisfies the Pythagorean theorem.

By the theorem:

`\begin{gathered} a^2=b^2+c^2 \\ a\text{ is the hypotenuse, the longest side.} \end{gathered}`

a. 12, 13, 16

`\begin{gathered} 16^2=12^2+13^2 \\ 256=144+169 \\ 256\\eq313 \end{gathered}`

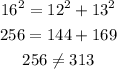
These side lengths do not form a right triangle.

b. 15, 20, 21

`\begin{gathered} 21^2=15^2+20^2 \\ 441=225+400 \\ 441\\eq625 \end{gathered}`

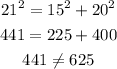
These side lengths do not form a right triangle.

c. 9,40,42

`\begin{gathered} 42^2=9^2+40^2 \\ 1764=81+1600 \\ 1764\\eq1681 \end{gathered}`

These side lengths do not form a right triangle.

d. 10, 24, 26

`\begin{gathered} 26^2=10^2+24^2 \\ 676=100+576 \\ 676=676 \end{gathered}`

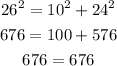
These side lengths form a right triangle since both sides of the equation are the same.