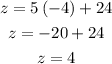Question

X+y+z=12x+4y+2z = -6-x+9y-3z=-49 Can someone please help me solve this system of equation?

Answer 1

Let's begin by listing out the information given to us:

`\begin{gathered} x+y+z=1 \\ 2x+4y+2z=-6 \\ -x+9y-3z=-49 \end{gathered}`

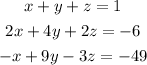
To solve this 3 variable equation, let's eliminate one of the variables

add equation 1 & 3, we have:

`\begin{gathered} x-x+y+9y+z-3z=1-49 \\ 10y-2z=-48 \\ Make\text{ z the }subject,we\text{ have:} \\ -2z=-10y-48 \\ divide\text{ through by -2} \\ z=5y+24 \end{gathered}`

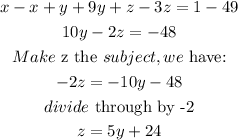
Substitute z into equation 1, 2 & 3

`\begin{gathered} x+y+5y+24=1 \\ x+6y=1-24 \\ x+6y=-23 \end{gathered}`

`\begin{gathered} 2x+4y+2\left(5y+24\right)=-6 \\ 2x+4y+10y+48=-6 \\ 2x+14y=-6-48 \\ 2x+14y=-54 \end{gathered}`

`\begin{gathered} -x+9y-3\left(5y+24\right)=-49 \\ -x+9y-15y-72=-49 \\ -x-6y=-49+72 \\ -x-6y=23 \end{gathered}`

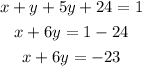
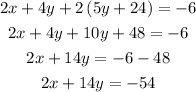
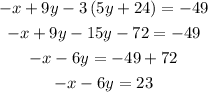
Solve as a simultaneous equation, we have:

`\begin{gathered} x+6y=-23 \\ 2x+14y=-54 \\ \text{Multiply the top equation by 2 \& subtract it from the bottom equation} \\ 2\cdot(x+6y=-23)\Rightarrow2x+12y=-46 \\ 2x+14y=-54-(2x+12y=-46) \\ 2x-2x+14y-12y=-54-(-46) \\ 2y=-8 \\ y=-4 \end{gathered}`

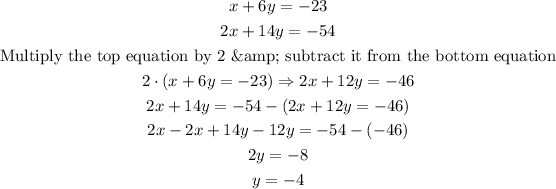
Substitute y = -4 into x + 6y = -23, we have:

`\begin{gathered} x+6\left(-4\right)=-23 \\ x-24=-23 \\ x=-23+24 \\ x=1 \end{gathered}`

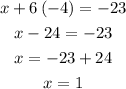
Substitute y = -4 into z = 5y + 24, we have:

`\begin{gathered} z=5\left(-4\right)+24 \\ z=-20+24 \\ z=4 \end{gathered}`