Question

The hands of a clock show 11:20. Express the obtuse angle formed by the hour and minute hands in radian measure.

Answer 1

`2.44\text{ }rad`

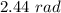
Step-by-step explanation

First, let us make a sketch of the clock:

We have that for a minute hand:

`1\text{ }min=6\degree`

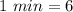
For hour hand:

`1\text{ }min=0.5\degree`

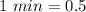
The hour and minute hand have their origin at 12.

At 11:20, the minute hand had moved 20 mins. This means that:

`20\text{ }min=20*6=120\degree`

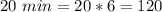
The hour hand had moved at 11 (and 20 mins more), which means:

`\begin{gathered} 11*60\text{ }min+20\text{ }min \\ \Rightarrow660\text{ }min+20\text{ }min \\ 680\text{ }min \end{gathered}`

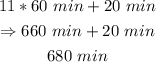
Hence, in 680 mins:

`\begin{gathered} 680*0.5 \\ \Rightarrow340\degree \end{gathered}`

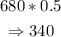
Therefore, the angle formed between 11 and 12 at 11:20 is:

`\begin{gathered} 360-340 \\ \Rightarrow20\degree \end{gathered}`

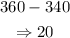
Hence, the angle formed at 11:20 is:

`\begin{gathered} 120\degree+20\degree \\ 140\degree \end{gathered}`

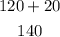
Now, let us convert to radians:

`\begin{gathered} 1\degree=(\pi)/(180)rad \\ 140\degree=140*(\pi)/(180)=2.44\text{ }rad \end{gathered}`

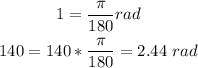
That is the obtuse angle formed in radians.