Question

Show that the points (3, 6), (0, -2), (-7, -5) and (-4, 3) are thevertices of a parallelogram.

Answer 1

Let

A(3,6) B(0,-2) C(-7,-5) D(-4,3)

Remember that

A parallelogram has opposite sides congruent and parallel

so

step 1

Find out the length of the side AB

using the formula to calculate the distance between two points

`\begin{gathered} AB=√((-2-6)^2+(0-3)^2) \\ AB=√(73) \end{gathered}`

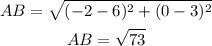
Find out the slope of the side AB

`m_(AB)=(-2-6)/(0-3)=(8)/(3)`

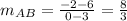
step 2

Find out the length of the side BC

`\begin{gathered} BC=√((-5+2)^2+(-7-0)) \\ BC=√(58) \end{gathered}`

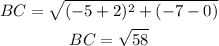
Find out the slope of the side BC

`m_(BC)=(-5+2)/(-7-0)=(3)/(7)`

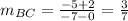
step 3

Find out the length of the side CD

`\begin{gathered} CD=√((3+5)^2+(-4+7)^2) \\ CD=√(73) \end{gathered}`

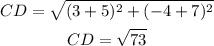
Find out the slope of the side CD

`m_(CD)=(3+5)/(-4+7)=(8)/(3)`

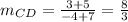
step 4

Find out the length of the side AD

`\begin{gathered} AD=√((3-6)^2+(-4-3)^2) \\ AD=√(58) \end{gathered}`

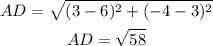
Find out the slope of the side AD

`m_(AD)=(3-6)/(-4-3)=(3)/(7)`

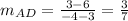
step 5

Compare the length of the sides

we have that

AB=CD

BC=AD

that means ----> opposite sides are congruent

Compare their slopes

mAB=mCD

mBC=mAD

that means ----> opposite sides are parallel

therefore

The given figure is a parallelogram