Given: The points a line intersects as shown below
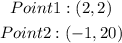
To Determine: The slope of the line in its simplest form
Solution
The formula for finding the slope of two points is as shown below
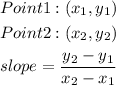
Let us apply the formula to the given points
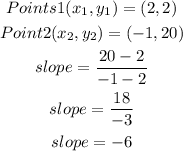
Hence, the slope of the line in simplest form is -6