Question

A basic cellular package costs $20/month for 60 minutes of calling with an additional charge of $0.20/minute beyond that time. The cost function C(x) for using x minutes would beIf you used 60 minutes or less, i.e. if if x≤60, then C(x)=20 (the base charge). If you used more than 60 minutes, i.e. (x−60) minutes more than the plan came with, you would pay an additional $0.20 for each of those (x−60) minutes. Your total bill would be C(x)=20+0.20(x−60). If you want to keep your bill at $50 or lower for the month, what is the maximum number of calling minutes you can use?

Answer 1

The maximum number of calling minutes you can use for $50 is 210 minutes.

To solve this, we have the function cost C(x) that depends on the amount of acalling munutes (x)

We want this cost to be $50 or lower. This means:

`\begin{gathered} CostFunction\colon C(x)=20+0.2(x-60) \\ Maximum\text{ value of 50:}C(x)\le50 \end{gathered}`

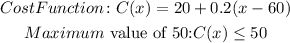
Then we can create an inequality:

`50\ge20+0.2(x-60)`

And now we can solve for x:

`\begin{gathered} 50\ge20+0.2(x-60) \\ (50-20)/(0.2)\ge x-60 \\ 150+60\ge x \\ x\le210\text{ minutes} \end{gathered}`

Thus, with $50 we can talk up to 210 minutes.

To be sure of the result, let's plug x = 210 in the function and it should give us a cost of C(210) = 50:

`\begin{gathered} x=210\Rightarrow C(210)=20+0.2(210-60) \\ C(210)=20+0.2\cdot150 \\ C(210)=20+30=50 \end{gathered}`

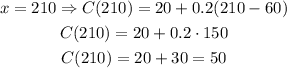
This confirms the result.