Given a parallelogram as shown below:
The formula to calculate the area of the parallelogram is given to be:
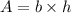
From the question provided, we have the following parameters:
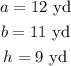
Therefore, we can use the formula to calculate the area as shown below:
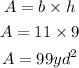
The area of the parallelogram is 99 squared yards (99 yd²).