Mathematics → Solid Figures → Volume
The volume of a cylinder is:
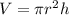
In this question,
r = 2 ft (4/2 =2)
h = 5 ft
Then, the volume of the cylinder is (Vc):
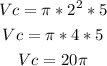
Using π = 3:
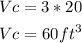
The volume of a rectangular prism (Vr) is:
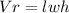
In this question:
l = 9 ft
w = 5 ft
h = 5 ft
Then, the volume of the rectangular prism is:
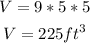
The volume of the object (V) is the sum of the volumes:
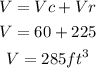
Answer: 285 ft³.