Question

Evaluate 1312e 4 Sov? 3x²x3 dx (Type an exact answer.)

Answer 1

We have to solve the integral:

`\int ^4_03x^2e^(x3)dx`

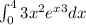
We will apply a variable substitution in order to simplify the solution. We have a hint when we see that the derivative of x^3 is 3x^2, that is part of the factors.

`\begin{gathered} u=x^3\Rightarrow du=(3x^2)dx \\ x=0\Rightarrow u=0^3=0 \\ x=4\Rightarrow u=4^3=64 \end{gathered}`

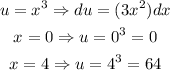
Then, we can write:

`\int ^4_03x^2e^(x3)dx=\int ^4_0e^(x3)(3x^2)dx=\int ^(64)_0e^udu`

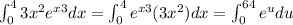
Then, we have a simpler integral to solve:

`\int ^(64)_0e^udu=e^u+C=e^(64)-e^0=e^(64)-1`

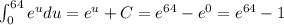
The exact solution is e^64-1.