Given: An arithmetic sequaence has the following parameters
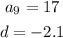
To Determine: The sum of the first 31st term.
Please note that the sum of the first 31st term is represented as
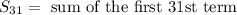
The formula for the finding the n-term of an arithmetic sequence (AP) is

Since, we are given the 9th term as 17, we can calculate the first term a, as shown below:

Calculate the sum of the first 31st term.
The formula for finding the first n-terms of an arithmetic series is given as
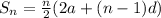
We are given the following:
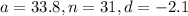
Substitute the given into the formula:
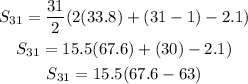
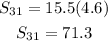
Hence, the sum of the first 31st term of the A.P is 71.3, OPTION D