Question

A small object of mass 0.500 kg is attached by a 0.440 m-long cord to a pin set into the surface of a frictionless table top. The object moves in a circle on the horizontal surface with a speed of 5.34 m/s.What is the magnitude of the radial acceleration of the object? What is the tension in the cord?

Answer 1

The magnitude of the radial acceleration of the object is 64.07 m/s² and the tension in the cord is 32.03 N.

Step-by-step explanation:

The magnitude of the radial acceleration of the object can be calculated using the formula:

ar = v² / r

Where ar is the radial acceleration, v is the speed of the object, and r is the radius of the circular path. Plugging in the given values:

ar = (5.34 m/s)² / 0.440 m = 64.07 m/s²

Therefore, the magnitude of the radial acceleration is 64.07 m/s².

The tension in the cord can be calculated using the formula:

T = m * ar

Where T is the tension in the cord and m is the mass of the object. Plugging in the given values:

T = (0.500 kg) * (64.07 m/s²) = 32.03 N

Therefore, the tension in the cord is 32.03 N.

Answer 2

Given data:

* The mass of the object attached is m = 0.5 kg.

* The radius of the circle is r = 0.44 m.

* The speed of the object moving in circular motion is v = 5.34 m/s.

Solution:

(a). The radial acceleration of the object is also known as the centripetal acceleration of the object.

The value of centripetal acceleration in terms of the velocity of the object is,

`a_c=(v^2)/(r)`

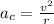
Substituting the known values,

`\begin{gathered} a_c=(5.34^2)/(0.44) \\ a_c=64.8ms^(-2) \end{gathered}`

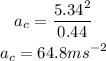
Thus, the radial acceleration of the object is 64.8 meters per second squared.

(b). The tension in the chord is equivalent to the centripetal force acting on the object which helps it to move in the circular motion.

Thus, the tension acting on the chord is,

`F=ma_c`

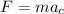
Substituting the known values,

`\begin{gathered} F=0.5*64.8 \\ F=32.4\text{ N} \end{gathered}`

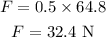
Thus, the tension acting in the chord is 32.4 N.