Given:
Initial velocity, vi = 41.0 m/s
Mass of ball, m = 195 g = 0.195 kg
Final velocity, vf = 37.0 m/s
Assuming the ball is moving horizontally just before and after collision with the bat, let's solve for the following:
• (A). What is the impulse delivered to the ball by the bat?
To find the impulse, apply the change in momentum formula:
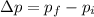
Where:
pi is the initial momentum = -mvi
pf is the final momentum = mvf
Thus, we have:
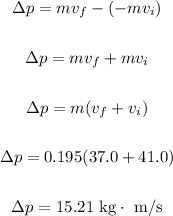
Impulse can be said to equal change in momentum.
Therefore, the impulse delivered to the ball by the bat is 15.21 kg.m/s away from the bat.
• (B). If the bat and ball are in contact for 3.00 ms, what is the magnitude of the average force exerted on the ball by the bat?
Apply the formula:

Rewrite the formula for force:

Where:
time = 3.00 m/s
impulse = 15.21 kg.m/s
Hence, we have:
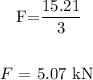
Therefore, the magnitude of the average force exerted on the ball by the bat is 5.07 kN away from the bat.
ANSWER:
(A). 15.21 kg.m/s away from the bat
(B). 5.07 kN.