Question

I need help with this question involving the Cartesian plane will post pic

Answer 1

The graph of f(x) is a parabola with "arms up"

The vertex of the parabola is (0,-3)

Then we can know all the problem ask us:

increasing: (-3, infinity)

decreasing: (minus infinty, -3)

DNE maximum, beacuase it's arbitrarily large.

The minimum is the vertex: minimum of -3 at x = 0

The domain is all real numbers

The range is [-3, infinity)

-------------------------------------------------------------------------------------------------------------------------------------------------------------

To know the shape of a parabola you want to look 2 things. The standar formula of a parabola is:

`f(x)=ax^2+b`

We focus on a and b. Always will be a squared x, but a and b vary. a lot

A tell us if the parabola has it's arms up or down. If is positive, has arms up. If it's negative, arms down.

Also, this isn't something "strictly mathematical" but can tel you is the parabola is thin or fat.

Now b tells us what happends when x=0. If b is positive, the vertex will be "rised up". If b is negative, the vertex will be "pulled down"

When you get relatively confident, you can watch a and b, and based on their sign and how big they are, you can make a really good idea how the graphic is.

All the information the problem ask, you can get it by those numbers.

To know how wide is a parabola, you need to look at a. Let's supose a = 100. This is a very big number, si if I plug in an x, the function will square it and multiply it by 100 right? Then the function will be very thin. For an x very low, the function will be very great. Example: f(x)=100x^2 if I put x = 1 then I have to square it, and multipli it by 100: 1^2*100=100

Now let's copare this with an smaller a. Suppose a =2. Then if I plug x = 1 I get:

`2x^2\text{ at x =1 }\Rightarrow f(1)=2\cdot1^2=2`

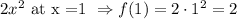
For the same value of x, the first function is 100 and the second 2