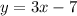Question

I need help with my algebra

Answer 1

We have the next equation line:

`3x-y\text{ = 5}`

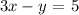
We need to solve the equation for y to get the equation form

`-y\text{ =5-3x}`

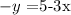
Multiply the equation by -1

`(-1)-y\text{ =(-1)(5-3x)}`
`y\text{ = -5+3x}`

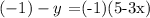
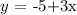
Where the y-intercept is -5 and the slope is 3x.

To find the line parallel we need to know that the parallel lines have the same slope.

The parallel line also intercepts y at point (0,-7).

`y=mx+b`

Replace the slope=m = 3

and the y-intercept is -7.

So the parallel line is:

`y=3x-7`