Question

A bag contains 8 red marbles, 7 blue marbles and 6 green marbles. If three marbles are drawn out of the bag without replacement, what is the probability, to the nearest 10th of a percent, that all three marbles drawn will be red?

Answer 1

Given the question, the following are the solution steps to answer the question.

STEP 1: Write the formula for probability

`Probability=\frac{number\text{ of required outcomes}}{number\text{ of total possible outcomes}}`

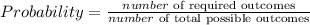
STEP 2: Write the outcomes of the events

`\begin{gathered} number\text{ of red marbles}\Rightarrow n(red)\Rightarrow8 \\ number\text{ of blue marbles}\Rightarrow n(blue)\Rightarrow7 \\ number\text{ of green marbles}\Rightarrow n(green)\Rightarrow6 \\ number\text{ of total marbles}\Rightarrow n(total)\Rightarrow21 \end{gathered}`

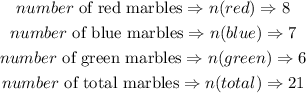
STEP 3: Write the formula for getting the probability that all three marbles drawn will be red

`Pr(Red\text{ and Red and Red\rparen}\Rightarrow Pr(red)* Pr(red)* Pr(red)`

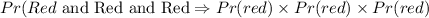
STEP 4: Calculate the probability

`\begin{gathered} Pr(all\text{ three are reds\rparen}\Rightarrow(8)/(21)*(7)/(20)*(6)/(19) \\ =(336)/(7980)=0.042105263 \\ To\text{ percentage will be to multiply by 100} \\ 4.210526316\% \\ To\text{ the nearest tenth will be:} \\ \approx4.2\% \end{gathered}`

Hence, the probability, to the nearest 10th of a percent, that all three marbles drawn will be red is 4.2%