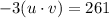Question

Can u please help me solve? I'm reviewing for finals.

Answer 1

Given:

Consider the given graph as a reference of the solution.

To find:

`-3(u\cdot v)`

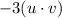
Step-by-step explanation:

By analyzing the graph, we can define the coordinate of vector u and v:

`\[\begin{align} & \vec{u}=(-8,-9)-(0,0)=(-8,-9) \\ & \vec{v}=(3,7)-(0,0)=(3,7)\end{align}\]`

Now, let perform the dot product of two vectors,

`\begin{gathered} u\cdot v=(-8,-9)\cdot(3,7) \\ u\cdot v=(-8)(3)+(-9)(7) \\ u\cdot v=-24-63 \\ u\cdot v=-87 \end{gathered}`

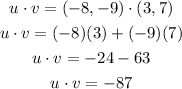
Now, perform the required operation,

`\begin{gathered} -3(u\cdot v) \\ =-3(-87) \\ =261 \end{gathered}`

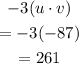
Final answer:

Hence, the required solution is:

`-3(u\cdot v)=261`