Answer:
A(-1,4) and B(2,0)
Explanation:
The quadratic parabola equation is represented as;
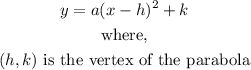
Therefore, if the given vertex (2,-5) and the other given point (-1,-1), substitute into the equation and solve for the constant ''a'':

Hence, the equation for the parabola:
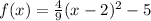
Now, for the line since it is a horizontal line, the equation would be:
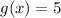
Then, for (f+g)(x):
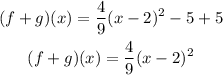
Then, the graph for the composite function and the points that lie on the graph:
A(-1,4) and B(2,0)