Given:
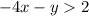
Consider the line,
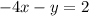
Find the points on the line,
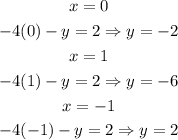
The graph of the line is,
Now, find the region for inequality.
Consider any point from the right and the left side of the line and check which side satisfies the inequality.
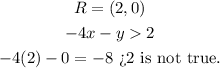
And,
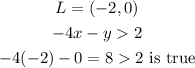
Therefore, the graph of the inequality is,
Note that inequality does not contain boundary points.