We have the following inequality
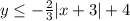
We must graph this inequality, In order to understand this I will explain term by term
But first, we must remember that in mathematics, the absolute value or modulus of a real number x, denoted by |x|, is the non-negative value of x regardless of the sign, positive or negative. This must be taken into account for the |x+3| term.
That is to say that the value will always be assumed by its magnitude and we will tend to have the same behavior on both the negative and positive x-axis.
Taking this into account and that the slope is -2/3 the graph would look like this:
Now, we must remember two rules of function translation, these are as follows:
y = f(x) original funtion
y = f(x+c) it is moved horizontally "c" units to the left
y = f(x)+c it moves vertically "c" units upwards
So taking into account these rules our graph is shifted 3 units to the left and 4 units upwards.
In conclusion, this graph looks like this: