Answer:
0.834
Explanations:
The formula calculating the z-score is expressed as:

Given the following parameters
• x1 = 49.55
,
• x2 = 73.35
,
• mean μ = 57inches
,
• standard deviation σ = 7.3in
Convert the x-values to z-score

For z2;
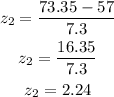
Determine the required probability
[tex]\begin{gathered} P(-1.02Hence the
probability that the
height of a randomly chosen child is between 49.55 and 73.35 inches is
0.834