We know we're dealing with two dice. Since each die has 6 different possibilities, the outcomes of rolling two dice are given by:
6 × 6, which is 36. This will be our denominator.
How many ways can we get 9 or 12 with two dices?
For a sum of 9:
3 + 6 = 9
4 + 5 = 9
There are two possibilities.
For a sum of 12:
6 + 6 = 12
There is only one possibility.
Summing it up, there are 3 possibilities to get a sum of 9 or 12 with the two dice.
The events are independent events since neither of them can ever occur at the same time.
Thus, the probability will be:

We get,
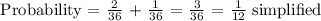
Therefore, the probability is 1/12.