Question

Find all critical points of the function f(x) = x^3 + 5x^2 - 7x - 3.The critical point(s) is(are) =

Answer 1

We are given:

`f(x)=x^3+5x^2-7x-3`

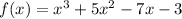
Now, we know that in order to determine the critical points we derivate and the derivative is then equal to 0, that is:

`f^(\prime)(x)=3x^2-10x-7=0`

Now, we solve for x, that is:

`3x^2+10x-7=0\Rightarrow x=\frac{-(10)\pm\sqrt[]{(10)^2-4(3)(-7)}}{2(3)}`
`\Rightarrow\begin{cases}x=-\frac{5+\sqrt[]{46}}{3}\Rightarrow x\approx-3.9 \\ \\ x=\frac{-5+\sqrt[]{46}}{3}\Rightarrow x\approx0.6\end{cases}`

So, the critical points of the function are:

`\begin{cases}x=-\frac{5+\sqrt[]{46}}{3} \\ \\ x=\frac{-5+\sqrt[]{46}}{3}\end{cases}`

Now, we determine the y-components of the points, that is:

`\begin{cases}f(-\frac{5+\sqrt[]{46}}{3})=(-\frac{5+\sqrt[]{46}}{3})^3+5(-\frac{5+\sqrt[]{46}}{3})^2-7(-\frac{5+\sqrt[]{46}}{3})-3\Rightarrow f(-\frac{5+\sqrt[]{46}}{3})=41.03608735 \\ \\ f(\frac{-5+\sqrt[]{46}}{3})=(\frac{-5+\sqrt[]{46}}{3})^3+5(\frac{-5+\sqrt[]{46}}{3})^2-7(\frac{-5+\sqrt[]{46}}{3})-3\Rightarrow f(\frac{-5+\sqrt[]{46}}{3})=-5.184235498\end{cases}`

So, the two critical points are:

`(-\frac{5+\sqrt[]{46}}{3},41.03608735)`

and:

`(\frac{-5+\sqrt[]{46}}{3},-5.184235498)`

This can be seing as follows: