The formula to calculate compound interest is given to be:
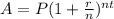
where:

The following parameters are given in the question:
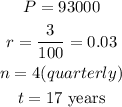
We can substitute these values into the formula to calculate the final amount as follows:
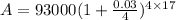
Solving, we get:
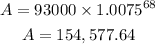
The amount after 17 years is $154,577.64