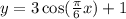Solution:
Given a cosine function graph;
The general cosine function is
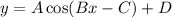
Where
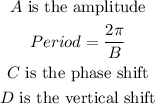
From the graph,
The midline is y = 1
The amplitude, A, is
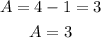
The amplitude, A is 3
Where,

The phase shift, C = 0, and the vertical, D, is 1
Thus, the equation of the graph is
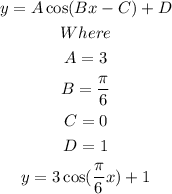
The graph is shown below
Hence, the equation is