Question

graph a line that is parallel to the given line. determine the slope of the given line and the one you graphed in simplest form. click and drag on the graph to draw a line. Click and drag to plot a parallel line. The line will change colors when a parallel or perpendicular line is drawn accurately.

Answer 1

Choosing two points of the line given ( Lg ):

• A( ,0, -4, )

,

• B( -,1.5, 0, )

Procedure:

0. Finding the slope ( ,m ,) of ,Lg:

`m_(Lg)=(y_2-y_1)/(x_2-x_1)`
`m_(Lg)=\frac{0_{}-(-4)_{}}{-1.5_{}-0_{}}=(4)/(-1.5)=-(8)/(3)`
`m_(Lg)=-(8)/(3)`

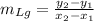
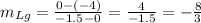
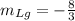
Also, based on point (0, -4), we can determine the intersection in y - axis ( b = -4). Therefore, the equation of the line given is:

`y=mx+b`
`y=-(8)/(3)x-4`

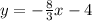
To determine the parallel slope ( mp ), we know that parallel lines have the same slope:

`m_p=m_(Lg)=-(8)/(3)`

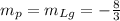
For the new graph, you would have to choose a different parameter b, all the equation would be the same except b. Choosing b = 3 as an example:

`y=-(8)/(3)x+3`

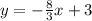
Answer:

• Original slope: -8/3

,

• Parallel slope: -8/3