Question

At the farmer’s market, Joan bought apples at $1.20 per pound, cherries for $2.00 per pound and pears for $0.80 per pound. She bought a total of 9 pounds of fruit for $11.00. Joan bought twice as many pounds of apples than cherries. Let A be the weight of the apples, C be the weight of the cherries, and P be the weight of the pears. Formulate a system of equations to determine how many pounds of each type of fruit were bought. Do Not Solve.

Answer 1

We have here a case in which we need to translate a problem into algebraic expressions to solve a problem, and we have the following information from the question:

• We have that Joan bought:

0. Apples at $1.20 per pound

,

1. Cherries at $2.00 per pound

,

2. Pears at $0.80 per pound

• We know that she bought a total of 9 pounds of fruit.

,

• We also know that she spent $11.00 for the 9 pounds of fruit.

,

• Joan bought twice as many pounds of apples than cherries.

We need to label weights as follows:

• Weight of apples ---> A

,

• Weight of cherries ---> C

,

• Weight of pears ---> P

Now to find a system of equations to determine the number of pounds of each type of fruit was bought, we can proceed as follows:

1. We know that if we multiply the price of the fruit per pound by the weight in pounds, we will obtain the amount of money Joan spent in total. Then we have:

`1.20a+2.00c+0.80p=11.00\rightarrow\text{ \lparen First equation\rparen}`

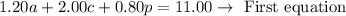
2. We also know that the total weight of the fruits was equal to 9 pounds. Then we can translate it into an algebraic expression as follows:

`a+c+p=9\rightarrow(\text{ Second equation\rparen}`

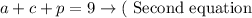
3. And we know that Joan bought twice as many pounds of apples than cherries, and we can translate it as follows too:

`\begin{gathered} 2a=c \\ \\ \text{ If we subtract c from both sides of the equation, we have:} \\ \\ 2a-c=c-c \\ \\ 2a-c=0\text{ \lparen Third equation\rparen} \end{gathered}`

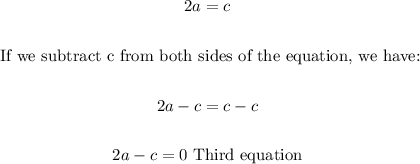
Now we have the following equations:

`\begin{gathered} 1.20a+2.00c+0.80p=11.00 \\ \\ \begin{equation*} a+c+p=9 \end{equation*} \\ \\ \begin{equation*} 2a-c=0 \end{equation*} \end{gathered}`

Therefore, we have that the correct option is the first option:

• 1.20a + 2.00c + 0.80p = 11.00

• a + c + p = 9

,

• 2a - c = 0

[First option].