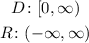Question

I need you to make a problem and solve it on the side and explain how explain it I’m making a practice test and I can show you examples of how I did the others This are the topics you can choose fromTopic 1: is the relation a function- domain and range Topic 2: zero is of a function

Answer 1

For topic (1), we have the following question:

Which of the following is a function: y=x² or x=y²?

Identify domain and range of each equation.

We can identify a given relation if it is a function or not by identifying the number of possible values of y.

The equations below are both relations.

`y=x^2\text{ and }x=y^2`

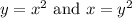
However, only one of them is a function.

For the first equation, note that for each value of x, there is only one value of y. Some of the points on the equation are as follows.

`\begin{gathered} x=-2 \\ y=x^2^{} \\ y=(-2)^2=4 \\ \\ x=0 \\ y=x^2 \\ y=0^2=0 \\ \\ x=2 \\ y=x^2 \\ y=2^2 \\ y=4 \end{gathered}`

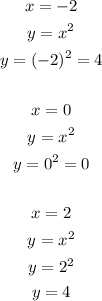
Thus, the equation passes through the following points.

`(-2,4),(0,0),(2,4)`

Notice that no value of x is repeated. Therefore, the given relation is a function.

We can also determine it using graphs. The image below is the graph of the first equation.

If we test it using the vertical line test, no vertical line can pass through the graph twice. Therefore, it shows that the equation is a function.

On the otherhand, the other equation is not a function. This is because when we substitute -2 and 2 to the value of y, we will have the same value of x, which is equal to 4.

`\begin{gathered} y=-2^{} \\ x=y^2 \\ x=(-2)^2=4 \\ \\ y=2 \\ x=y^2^{} \\ x=2^2=4 \end{gathered}`

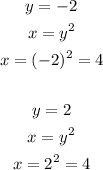
Since there are two values of y for only one value of x, the equation must not be a function.

To illustrate this using its graph, we can notice that the vertical line below passes through two points on the graph when x=4.

Therefore, the second equation is not a function.

As for the domain and range, we can obtain it from both graphs.

The domain the set of all possible values of x. Thus, for the first equation, since it extends indefinitely to the left and right, the domain must be from negative infinity to positive infinity.

`D_1\colon(-\infty,\infty)`

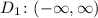
On the otherhand, since the second equation extends indefinitely to the right from 0, the domain must be from 0 to positive infinity, inclusive.

`D_2\colon\lbrack0,\infty)`

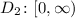
As for the range, it is the set of all possible values of y.

Thus, for the first equation, since the graph extends indefinitely upwards from 0, the range must be from 0 to positive infinity, inclusive.

`R_1\colon\lbrack0,\infty)`

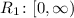
On the otherhand, the graph of the second equation extends indefinitely upwards and downwards. Thus, its range must be from negative infinity to positive infinity.

`R_2\colon(-\infty,\infty)`

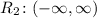
To summarize, here are the questions and the answers for each question.

Which of the following is a function: y=x² or x=y²?

Answer: y=x²

Identify domain and range of each equation.

Answer:

For y=x²:

`\begin{gathered} D\colon\text{ (-}\infty,\infty\text{)} \\ R\colon\lbrack0,\infty) \end{gathered}`

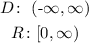
For x=y²:

`\begin{gathered} D\colon\lbrack0,\infty) \\ R\colon(-\infty,\infty) \end{gathered}`