Question

All i need is for question 14 to be answered please help

Answer 1

Given

The path of particle 1 is,

`x(t)=3t-6,\text{ }y(t)=t^2-2t`

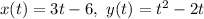
And, the path of second particle is,

`x(t)=√(t+6),\text{ }y(t)=-3+2t`

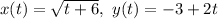
To model the path of the two particles in cartesian form and to find whether, the two particles collide.

Step-by-step explanation:

It is given that,

The path of the first particle is,

`x(t)=3t-6,\text{ }y(t)=t^2-2t`

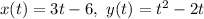
That implies,

`x=2t-6,\text{ }y=t^2-2t`

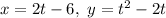
Consider,

`\begin{gathered} x=2t-6 \\ 2t=x+6 \\ t=(x+6)/(2) \end{gathered}`

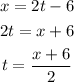
Therefore,

`\begin{gathered} y=((x+6)/(2))^2-2((x+6)/(2)) \\ y=(x^2+12x+36)/(4)-(2x+12)/(2) \\ y=(x^2+12x+36-2(2x+12))/(4) \\ y=(x^2+12x+36-4x-24)/(4) \\ y=(x^2+8x+12)/(4)\text{ \_\_\_\_\_\_\_\_\_\_\lparen1\rparen} \end{gathered}`

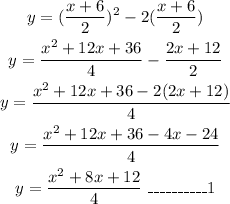
Also, the path of second particle is,

`x(t)=√(t+6),\text{ }y(t)=-3+2t`

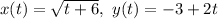
That implies,

`x=√(t+6),\text{ }y=-3+2t`

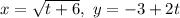
Consider,

`\begin{gathered} y=-3+2t \\ 2t=y+3 \\ t=(y+3)/(2) \end{gathered}`

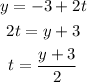
Therefore,

`\begin{gathered} x=√(t+6) \\ \Rightarrow x^2=(t+6) \\ \Rightarrow x^2=((y+3)/(2))+6 \\ \Rightarrow x^2=(y+3+12)/(2) \\ \Rightarrow2x^2=y+15 \\ \Rightarrow y=2x^2-15\text{ \_\_\_\_\_\lparen2\rparen} \end{gathered}`

Hence, y=(x^2+8x+12)/4, y=2x^2-15 are the paths of the two particles respectively.

The graph of the path of the two particles are,

From, this it is clear that the particle collide at the points (-2.686, -0.568) and (3.829, 14.324).