SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Get the angles of the hexagon
The internal angles of an hexagon is given as:
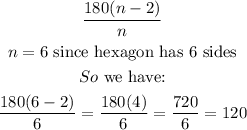
Therefore each angle of the hexagon is 120 degrees.
STEP 2: find the length of the sides
We remove the right triangles as seen below:
Using the special right triangles, we have:
STEP 3: find the area of the extracted triangle above
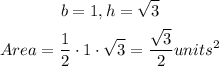
Since there are two right triangles, we multiply the area by 2 to have:
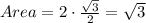
There are two triangles(both sides), therefore the total area of the shaded area will be:
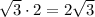
STEP 4: Find the area of the whole hexagon

STEP 5: Find the probability

Hence, the probability that the dart hits one of the shaded areas is approximately 0.3333