Given:
Flipping a coin twice.
Required:
We need to find the likelihood of flipping heads twice in a row.
Step-by-step explanation:
The sample space = All possible outcomes.
The sample space, S= {TT,TH,HT,HH}
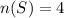
Let A be the event of flipping heads twice..
The favorable outcomes = flipping heads twice.
The favorable outcomes ={HH}
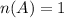
Consider the probability formula.
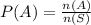
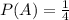
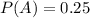
The probability of flipping heads twice in a row is 0.25 which is a close value to the number 0.
This event happens least likely.
Final answer:
Flipping heads twice in a row is the least likely.
The probability of flipping heads twice in a row is 0.25.