Given the equation:

Let's identify the type of polar graph for the equation.
To identify the type of polar graph, use the formula below to get the Cartesian form:
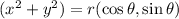
Thus, we have:
![(x^2+y^2)=3\sqrt[]{x^2+y^2}-5x](https://img.qammunity.org/2023/formulas/mathematics/college/itshqazwskbeci1mhv8ttmw60uewg0beve.png)
We have the graph of the equation below:
We can see the graph forms a Limacon with an inner loop.
Therefore, the type of polar graph for the given equation is a limacon with inner loop.
ANSWER: