Question

A convenience store manager notices that sales of soft drinks are higher on hotter days, so he assembles the data in the table. (a) Make a scatter plot of the data. (b) Find and graph a linear regression equation that models the data. (c) Use the model to predict soft-drink sales if the temperature is 95°F.

Answer 1

ANSWER and EXPLANATION

a) First we have to make a scatter plot. We do this by plotting the calues of High Temperature on the x axis and Number of cans sold on the y axis:

b) We want to find and graph the linear regression equation that models the data.

The linear regression equation will be in the form:

y = a + bx

`\begin{gathered} \text{where} \\ a\text{= }\frac{(\sum ^{}_{}y)(\sum ^{}_{}x^2)\text{ - (}\sum ^{}_{}x)(\sum ^{}_{}xy)}{n(\sum ^{}_{}x^2)\text{ }-\text{ (}\sum ^{}_{}x)^2} \\ \text{and b = }\frac{n(\sum ^{}_{}xy)\text{ - (}\sum ^{}_{}x)(\sum ^{}_{}y)}{n(\sum ^{}_{}x^2)\text{ }-\text{ (}\sum ^{}_{}x)^2} \end{gathered}`

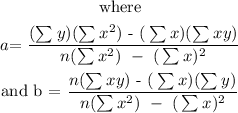
We have from the question that:

x = High Temperature

y = Number of cans added

So, we have to find xy and x^2. We will form a new table:

Now, we will find a and b:

`\begin{gathered} a\text{ = }\frac{(4120)(39090)\text{ - (}554)(297220)}{8(39090)\text{ }-554^2} \\ a\text{ = }\frac{\text{ 161050800 - 164659880}}{312720\text{ - 306916}} \\ a\text{ = }(-3609080)/(5804) \\ a\text{ }\cong\text{-62}2 \end{gathered}`
`\begin{gathered} b\text{ = }\frac{8(297220)\text{ - (554})(4120)}{5804} \\ b\text{ = }\frac{2377760\text{ - 2282480}}{5804} \\ b\text{ = }(95280)/(5804) \\ b\text{ }\cong\text{ 16} \end{gathered}`

Therefore, the linear regression equation is:

y = -622 + 16x

Now, let us graph it using values of x (High Temperature):

That is the Linear Regression Graph.

c) To predict soft drink sales if the temperature is 95 degrees Farenheit, we will put the x value as 95 and find y. That is:

y = -622 + 16(95)

y = 898

The model predicts that 898 cans of soft drinks will be sold when the High Temperature is 95 degrees Farenheit.