Question

What is the equation in slope-intercept form of the line that passes through the points (-4,8) and (12,4)?

Answer 1

y = -0.25 + 7

Step-by-step explanation

The line passes through the points (-4, 8) and (12, 4).

The slope-intercept form of a linear equation is written as:

y = mx + c

where m = slope

c = y intercept

First, we have to find the slope of the line.

We do that with formula:

`\begin{gathered} m\text{ = }(y_2-y_1)/(x_2-x_1) \\ \text{where (x}_1,y_1)\text{ = (-4, 8) } \\ (x_2,y_2)\text{ = (12, 4)} \end{gathered}`

Therefore, the slope is:

`\begin{gathered} m\text{ = }\frac{4\text{ - 8}}{12\text{ - (-4)}}\text{ = }\frac{-4}{12\text{ + 4}}\text{ = }(-4)/(16)\text{ = }(-1)/(4) \\ m\text{ = -0.25} \end{gathered}`

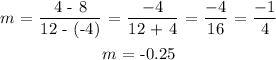
Now, we use the point-slope method to find the equation:

`\begin{gathered} y-y_{1\text{ }}=m(x-x_1) \\ \Rightarrow\text{ y - 8 = -0.25(x - (-4))} \\ y\text{ - 8 = -0.25(x + 4)} \\ y\text{ - 8 = -0.25x - 1} \\ y\text{ = -0.25x - 1 + 8} \\ y\text{ = -0.25x + 7} \end{gathered}`

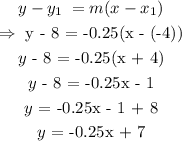
That is the equation of the line. It is not among the options.