Let's begin by listing out the information given to us:
Discount = 20%
Book prices: $2.50, $4.95, and $6.00
Taking discount with distribution, we have:
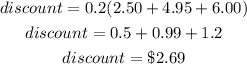
Taking discount without distribution, we have:
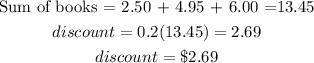
I think it is easier to not distribute. This is because it reduces significantly the chances of numerical error in computing